Saludos

                                              SALUDOS A TODOS



DESDE NUESTRO BLOGGER LE DAMOS LA BIENVENIDAS A TODOS AQUELLOS  QUE NOS PUEDEN VER DESDE EL SUYO, Y GRACIAS POR SU INTERÉS.ESTE BLOG CONSISTE EN DAR A CONOCER UN POCO CON LO QUE HEMOS APRENDIDO EN NUESTRA CLASE DE ATP(ÁLGEBRA DE TRANSFORMACIONES DEL PLANO),YA QUE ES UNA MATERIA FÁCIL,CREATIVA,DINÁMICA;PERO DE MUCHA PACIENCIA CUANDO SE REALICE CUALQUIER EJERCICIO QUE SE DE;INCLUSO PUEDE UNO HASTA PERDERSE;LO CUAL  SUCEDE SI NO SE ESTUDIA.ESPERO LE GUSTE COMO NOS GUSTO A NOSOTROS; AUNQUE AL PRINCIPIO NO NOS LATÍA PERO AL FINAL NOS FASCINO.  

Unidades

                                                    Unidades


Dentro de las unidades,tenemos lo que son:las transformaciones del plano e introducción del plano.

Estudiar las transformaciones en el plano es simplemente fascinante, pues hablamos de aprender a trabajar con figuras convexas o cóncavas en el plano, transformándolas de diversas maneras sin alterar su esencia.

No existe un único tipo de transformaciones en el plano, por lo que antes de entrar en detalle en cada una de ellas, aprenderlas y ejercitarlas comenzaremos por clarificarlas y comprender las diferencias entre ellas. 

Introducción de transformación lineales:es un conjunto de operaciones que se realizan sobre un vector,para convertirlo en otro vector.los espacios vectoriales son conjuntos con una estructura adicionales al saber sus elementos se pueden sumar y multiplicar por escalares del campo. 

                         

Definiciones Basicas

                                                 Definiciones Básicas

.Un movimiento en el plano es una transformación geométrica del plano que conserva los ángulos y las distancias (la forma y el tamaño). Se distinguen tres tipos de movimientos: Traslación, giro y simetría. 1.- TRASLACIÓN Definición: Se llama traslación T de vector libre AB a una transformación que asocia a cada punto P del plano otro punto P'=T(P) de manera que el vector PP' sea igual al vector AB. En esta escena se muestra una traslación de vector AB. Tanto AB como el segmento PQ se pueden mover. Un punto o una figura, es invariante por un movimiento (también se dice que es doble) , cuando se transforma en sí mismo al aplicarle dirección . GIROS Definición: Se llama giro de centro O y ángulo ß a un movimiento que hace corresponder a cada punto P otro punto P' tal que : d(O, P) =d (O, P') y ángulo(POP') = ß Cuando el ángulo de giro es de 180º se dice que es una simetría central de centro O. 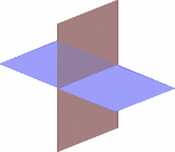SIMETRÍA Definición: Se llama simetría axial S, de eje e, a un movimiento que transforma un punto P en otro P' de modo que e es mediatriz del segmento PP', o lo que es lo mismo, d(P, e) = d(P', e) Propiedades del plano ℝ3[editar] Intersección de dos planos en un espacio tridimensional. Representación isométrica de dos planos perpendiculares. En un espacio euclidiano tridimensional ℝ3, podemos hallar los siguientes hechos, (los cuales no son necesariamente válidos para dimensiones mayores). O bien dos planos son paralelos, o bien se intersecan en una línea. O bien una recta es paralela a un plano, o bien se intersecta con el mismo en un punto, o bien está contenida en él. Dos rectas perpendiculares a un mismo plano son paralelas entre sí. Dos planos perpendiculares a una misma recta son paralelos entre sí. Entre un plano Π cualquiera y una recta no perpendicular al mismo existe sólo un plano tal que contiene a la recta y es perpendicular al plano Π. Entre un plano Π cualquiera y una recta perpendicular al mismo existen infinitos planos tales que contienen a la recta y son perpendiculares al plano Π.

Deslizamiento

                                   Deslizamiento 
En el deslizamiento tenemos al vector y rosa de los vientos. 
            

un vector (también llamado vector euclidiano o vector geométrico) es una magnitud física definida en un sistema de referencia que se caracteriza por tener módulo (o longitud) y una dirección (u orientación).¹​²​³​

En matemáticas se define un vector como un elemento de un espacio vectorial. Esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo y la dirección. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo. Los vectores en un espacio euclídeo se pueden representar geométricamente como segmentos de recta ${\displaystyle \mathbb {R} }$, en el plano ${\displaystyle \mathbb {R} ^{2}}$, o en el espacio ${\displaystyle \mathbb {R} ^{3}}$.

Algunos ejemplos de magnitudes físicas que son magnitudes vectoriales: la velocidad con que se desplaza un móvil, ya que no queda definida tan solo por su módulo que es lo que marca el velocímetro, en el caso de un automóvil, sino que se requiere indicar la dirección (hacia donde se dirige), la fuerza que actúa sobre un objeto, ya que su efecto depende además de su magnitud o módulo, de la dirección en la que actúa; también, el desplazamiento de un objeto, pues es necesario definir el punto inicial y final del movimiento.

 rosa de los vientos es un símbolo en forma de círculo que tiene marcados alrededor los rumbos en que se divide la circunferencia del horizonte. Su invención se atribuye al mallorquín Ramon Llull, aunque la descripción pormenorizada que da Plinio el viejo en libro II¹​ podría haber sido su referencia básica.

En las cartas de navegación se representa por 32 rombos (deformados) unidos por un extremo mientras el otro señala el rumbo sobre el círculo del horizonte. Sobre el mismo se sitúa la flor de lista con la que suelen representar el Norte, que se documenta a partir del siglo XV.

.

Simetria Central

                                        Simetria Central

​La simetría respecto de un punto de vista se le llama simetría central y "los puntos correspondientes". En una simetría central, los segmentos homólogos son iguales y la medida de los ángulos correspondientes también son iguales.

Ocho puntos P son simétricos respecto a la simetría O cuando OP = OP', esto es P y P' equidistan del centro de simetría.²​

Ejemplo 1:

Dibuja un círculo simétrico respecto del centro O del triángulo dado ABC.

Simetria Axial

                                 

Simetria Axial  
     

 La simetría axial (también llamada rotacional, radial o cilíndrica) es la simetría alrededor de un eje. Es el punto de traslación y rotación de modo que un sistema tiene simetría axial o axisimetría cuando todos los semiplanos tomados a partir de cierta mediatriz y conteniéndolo presentan idénticas características.También puede decirse que es una isometría indirecta e involutiva.

Dada una recta se llama simetría axial de eje al movimiento que transforma a un punto P en otro punto P' verificando que:

• El segmento PP' es perpendicular a ${\displaystyle \scriptstyle e}$.
• Los puntos P y P' equidistan del eje ${\displaystyle \scriptstyle e}$.

Dicho de otra forma el eje ${\displaystyle \scriptstyle e}$ es la mediatriz del segmento OP'.

La simetría axial no solo se presenta entre un objeto y su reflexión, pues muchas figuras que mediante una línea pueden partirse en dos secciones que son simétricas con respecto a la línea. Estos objetos tienen uno (o más) ejes de simetría.

La simetría axial se da cuando los puntos de una figura coinciden con los puntos de otra, al tomar como referencia una línea que se conoce con el nombre de eje de simetría. En la simetría axial se da el mismo fenómeno que en una imagen reflejada en el espejo.                                       

Rotacion

Rotacion:Este vocablo se deriva del latín “rotatio”. La rotación es la acción que puede ejercer un cuerpo de rodar o dar vuelta en su propio eje, el cual puede ser una línea o un punto que permanece fijo, el mismo es denominado eje de rotación.

La rotación es básicamente el movimiento de un cuerpo donde cambia su orientación, del mismo modo el cuerpo tiene la capacidad de que mientras va girando cualquier punto que pertenezca a él mantendrá la misma distancia con respecto al eje de rotación (a pesar de su movimiento), al culminar el giro o vuelta el cuerpo vuelve a su posición original, indicando que se ha realizado una rotación completa, la cual puede realizarse varias veces, es decir el mismo cuerpo puede girar alrededor de su eje en distintas oportunidades.